Chapitre 1 - Coordonnées d'un point du plan

Lire les coordonnées d'un point dans un repère.
Placer un point dans un repère, connaissant ses coordonnées.
Calculer les coordonnées du milieu d'un segment.
Calculer une distance.
Démontrer en géométrie.

IRepères et coordonnées d'un point dans le plan

1Repérage d'un point dans le plan

Un repère du plan est constitué de trois points $(O, I, J)$ ordonnés formant un triangle.

$O$ est l'origine
$(OI)$ est l'axe des abscisses et $OJ$ est l'axe des ordonnées
Si $\widehat{IOJ}$ est un angle droit, et que les distances $OI$ et $OJ$ sont égales, le repère est orthonormé

Un repère orthonormé

Des repères non orthonormés

Repérer un point M dans le repère $(O; I; J)$, c'est donner donner l'unique couple de nombres $(x_M; y_M)$ où $x_M$ est l'abscisse de $M$ et $y_M$ est l'ordonnée de $M$.

Ci-dessous, le repère est orthornormé. Les coordonnées de $M$ sont le couple $(x_M;y_M)$. Par lecture graphique, l'abscisse de A vaut 2 et son ordonnée vaut 1.

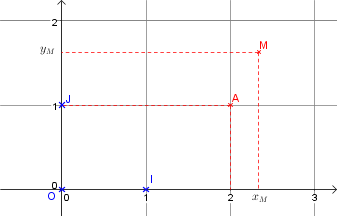
Sur l'axe des abscisses, on place un point $P$ au niveau de l'abscisse $x_M$ de M et sur l'axe des ordonnées on place un autre point $Q$ au niveau de l'ordonnée $y_M$. Alors $OPMQ$ est un parallélogramme.

Une manière abrégée de dire que $M$ a pour coordonnées le couple$(x_M;y_M)$ est : $$M (x_M;y_m)$$

Ci-dessous, le repère n'est pas orthornormé. On a $ A (2,2), B (-1;1)$ et $C (3,-1)$.

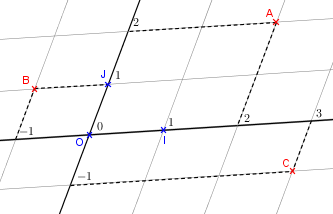
2Coordonnées du milieu d'un segment

Dans un repère, pour tracer précisément le milieu d'un segment $[AB]$, on peut en premier tracer le milieu des abscisses de$A$ et de $B$ sur l'axe des abscisses, puis faire de même sur l'axe des ordonnées

On trace ci-dessous le segment $[AB]$ où $ A (1,1), B (3;2)$. On appelle $(x_K;y_K)$ les coordonnées de $K$. Sur les axes, $x_K$ vaut $2$ et $y_K$ vaut $1,5$ :

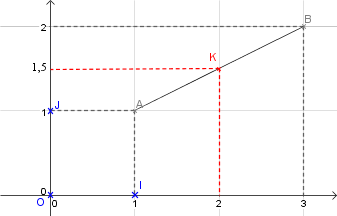
Une formule permet de calculer les coordonnées du point milieu avant de le tracer :

Prenons deux points $A$ et $B$ de coordonnées $(x_A;y_A)$ et $(x_B;y_B)$. Le milieu $M$ du segment $[AB]$ a pour coordonnées : $$(\frac{x_A + x_B}{2};\frac{y_A + y_B}{2})$$

L'absisse de $K$ est la moyenne des abscisses de $A$ et $B$
L'ordonnée de $K$ est la moyenne des ordonnées de $A$ et $B$

On vérifie en appliquant la formule que les coordonnées du milieu $K$ sont bien $(2;1,5)$ \[ \begin{aligned} x_K & = \frac{x_A + x_B}{2} =\frac{1+3}{2} = 2 \\ y_K & = \frac{y_A + y_B}{2} =\frac{1+2}{2} = 1,5 \end{aligned} \]

IIDistance entre deux points dans un repère orthonormé

Dans un repère orthonormé, on considère les points $A$ et $B$ de coordonnées $(x_A;y_A)$ et $(x_B;y_B)$. Alors la distance $AB$ peut être calculée par la formule : $$ AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2} $$

Sur l'exemple ci-dessous, $A (-1;1)$ et $B (3;4)$. En reproduisant avec $OI = OJ = 1 cm$ et en mesurant à la règle, il semble que $AB = 5 cm$

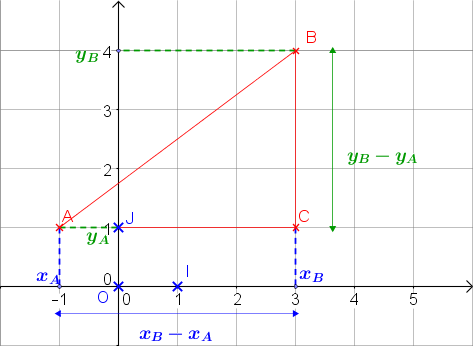On peut vérifier en appliquant la formule : \[ \begin{aligned} AB & = \sqrt{(3 - (-1))^2 + (4 - 1)^2}\\ AB & = \sqrt{4^2 + 3^2}\\ AB & = \sqrt{16 + 9}\\ AB & = \sqrt{25}\\ AB & = 5 \end{aligned} \]

On peut échanger les points $A$ et $B$, cela ne change rien à la distance car $AB=BA$. La formule reste donc correcte si l'on écrit $$ AB = \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$